Lasery v textilním průmyslu

Lasery nacházejí široké uplatnění napříč všemi výrobními odvětvími. Není tedy divu, že skvělých výsledků dosahuje i jejich použití v textilním průmyslu. Tak, jako existuje spousta typů laserů, existuje i spousta jejich různých aplikací. Lasery nabízejí širokou škálu výhod a mohou doplnit klasické techniky zpracování textilu. Těmi hlavními výhodami jsou přesnost zpracování, opakovatelnost a velké rozlišení při tvorbě detailních a komplikovaných tvarů. Dalším přínosem použití laserů je bezkontaktní zpracování látky (bez použití nástroje), které usnadňuje automatizaci výroby a udržuje konstantní kvalitu řezu.
Princip funkce
V textilním průmyslu se lasery používají zejména k řezání, gravírování a vytváření prostorového designu na látce. Obzvláště vhodné jsou vysokovýkonové liniové CO2 lasery. Lze ale použít i pevnolátkový (vláknový diodový) či excimerový laser, a to v závislosti na parametrech aplikace (např. dobrá absorpce dané vlnové délky laseru v materiálu specifické barvy).
Lasery jsou umístěné v plotterech, v zařízeních s rozmítací hlavou, či ve strojích, které obě tyto metody kombinují.
Konstruktér v počítačovém programu navrhne design, který se přenese do laserového výrobního stroje. Koncentrovaný laserový svazek je nasměrován na látku, na které vytvoří požadovaný vzhled odpařením či spálením textilních vláken. Laserová technologie nepoužívá žádný spotřební materiál kromě elektřiny a asistenčních plynů odfukujících vzniklé taveniny z místa řezu. Neposlední výhodou je i dlouhá životnost laserového zdroje, přičemž někteří výrobci garantují až 20.000 operačních hodin.
Metody práce s materiálem můžeme rozdělit následovně:
– Vybělení pigmentu
– Destrukce materiálu
– Fázová transformace
– Vitrifikace
– Karbonizování
– Roztavení
– Odpaření, odstranění horní vrstvy
Pro zpracování laserovým paprskem jsou vhodné technické a syntetické textilie (polyester, polyamid, fleece, filc, polyester, Aramid, Kevlar, plyš, síťovina, aj.) i přírodní materiály (bavlna, hedvábí, vlna, kůže). Jejich sledovanými parametry jsou zejména optické (odrazivost, absorpce, propustnost) a termo-fyzikální (koeficient tepelné vodivosti, měrné skupenské teplo, aj) vlastnosti. Uvedeme příklad polyesterových vláken. Při 80-90 °C vitrifikují, při 250 °C měknou, při 260 °C tají a při 350 °C se odpařují.
Dále se podíváme blíže na jednotlivé činnosti z textilního průmyslu a popíšeme, jak využívají laserová záření.
1. Řezání
Dělení materiálu je jednou ze základních činností v textilním průmyslu. Laser umožňuje řezat různé druhy, tvary a velikosti materiálů, včetně složitějších kontur, bez přípravy výsekových raznic. Snižuje spotřebu materiálu tím, že umožňuje nastavit minimální prořez (tzv. nesting technologie) a vytváří se tak méně odpadu. Řezání je bezkontaktní, není tedy třeba fixovat materiál a nedochází k jeho deformaci nebo poškození.

Obrázek 1: Rozdíl mezi řezáním laserovým svazkem a konvenčním nožem [1]
Řez je precizní, dokonalý, čistý a rychlý. Další výhodou je, že při řezání např. polyesteru laserový paprsek taví hrany a zabraňuje tak třepení, popř. současně utěsní okraje. Výrobní proces se tak zrychluje sloučením jednotlivých činností.
Laserové řezání je bezprašný proces, nicméně je nutné zajistit odsávání zplodin. Pro dosažení kvalitních neopálených okrajů a povrchu je vhodné používat asistenční plyn, distribuovaný do místa opracovávání.
2. Svařování
Laserové svařování textilií je technologie vytvářející nerozebíratelné spojení dvou shodných materiálů. Syntetické textilie, které se při určité teplotě taví, je možné svařovat laserem. Laserové svary nahrazují sešití nití. Svařování lze spojit s řezáním materiálu v jednom výrobním kroku. Výsledkem jsou dokonale zatavené hrany, které splňují i nejpřísnější normy na filtrační techniku.
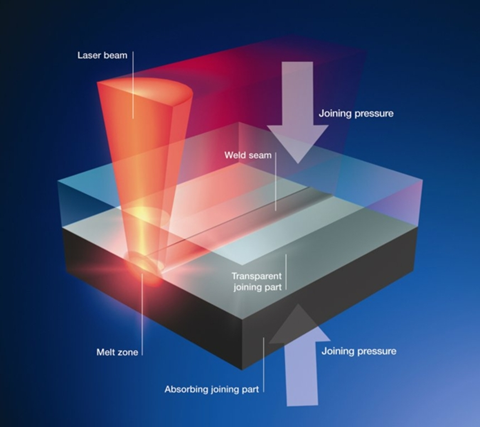
Obrázek 2: Princip laserového svařování [2]
Pro svařování se používají lasery vyzařující v IR spektru. Je-li potřeba svařit látku, která nepohlcuje IR záření, natiskne či nanese se na ni nejdříve stopa IR absorbéru, který následně reaguje s dopadajícím laserovým záření.
3. Značení a dekorace
Obecným cílem značení je identifikace, poskytnutí informace, vytvoření dekorace, či varování. Výhodou laserového značení je jeho snadné použití už při sledování životní cesty materiálu, který do výroby vstupuje. Značení laserem umožňuje dosahovat vysokých rychlostí zpracování. Technologie využívá laser jako tepelný zdroj, který sublimací odpaří barvu či část materiálu. Bez použití vody či dalších chemických látek lze dosáhnout vybělení materiálu či naopak škály odstupňovaného barevného odstínu (viz Obrázek 3) vhodné pro popis textilií. Značit se dají syntetické, přírodní i kompozitní materiály.

Obrázek 3: Barevný gradient dosažitelný laserovým svazkem [3]
Škála dekoračních technik je široká, od vyřezávaných, vypalovaných ornamentů, po povrchové úpravy typu seprání, 3D gravírování (pro materiály s vyšší tloušťkou) či vytváření barevných gradientů. Zároveň lze dekoraci s využitím laseru kombinovat s jinými metodami za účelem vytvoření jedinečného vzhledu. Na rozdíl od tisku je laserem možné vytvářet hmatové efekty.
Laserový paprsek tepelně ovlivňuje pouze malou část materiálu. Lze ho tak použít i na recyklované a přešívané oděvy s vysokou mírou úprav dle potřeb zákazníka.
4. Kontrola
Laserový paprsek umožňuje přesnou kontrolu a měření různých vlastností materiálů a objektů. Používá se například k detekci přetržení nití při výrobě osnovy. V kombinaci se softwarem lze snímat a vyhodnocovat kvalitu materiálu a optimalizovat dle ní umístění objektů. Ke skenování se používá laserový osvětlovač, který postupně snímá části látky a detektorem se zachycuje odražené záření, které se následně datově zpracuje.
Dalším použitím laserů je jejich jednoduchá aplikace v zaměřovacích křížích používaných k zarovnání výrobků před potiskem, ke srovnání látky se střihem, či jako vodítek pro rovný šev.
Typické aplikace
– Oděvní průmysl – široké spektrum materiálů, zpracování látek na roli, sportovní oblečení, kožené boty, tašky
– Džínovina – efekt seprání, 3D gravírování, gradienty

Obrázek 4: Postup zpracování džínoviny laserem [4]
– Sportovní vybavení – padáky, stany, plachty, spací pytle
– Hračky a dekorační předměty

Obrázek 5: Ukázka laserového řezání plyše [5]
– Bytové textilie – nábytkové potahy, závěsy, stínidla, slunečníky, koberce, rohože z uhlíkových vláken
– Filtrační materiály – FFP filtry, medicínské respirátory, bio filtry, potravinářské filtry, vzduchotechnické filtry, filtrační látky
– Automobilový a letecký průmysl – potahy, bezpečnostní pásy, airbagy
– Technické textilie – potahy, plachty, bannery, izolační materiál
– Polyesterové suché zipy – rychloupínací brusný papír

Obrázek 6: Netřepivá hrana vytvořená laserovým řezáním [6]
Nevýhody použití laserových systémů v textilním průmyslu
Hlavní nevýhodou použití laserů v textilním průmyslu jsou vysoké vstupní investice a náklady na zavedení výroby.
Výrobní proces je omezen na zpracování pouze určitých typů látek a barev. Zpracování různých materiálů také vyžaduje pečlivou přípravu v nastavení parametrů. Například při zpracování organických textilií laserem může řezná hrana vykazovat nežádoucí zabarvení. U specifických materiálů, jako je džínovina, lze využít LSF test (Light Sensitive Fabric test), při němž se vzorek materiálu otestuje laserovými technologiemi, čímž získáme přesná data, která se použijí k výběru a nastavení optimálních pracovních podmínek.
V neposlední řadě je třeba dbát i na státní regulační a bezpečnostní pravidla.
Reference
- Spacer fabric – laser cutting machines for the automotive industry (eurolaser.com)
- Laser welding of textiles | textile network (textile-network.com)
- Compact Super Laser Marking Technology – Jeanologia
- Twin Super Laser Marking Technology – Jeanologia
- Laser cutting of a teddy bear made of plush (polyester fabric) (eurolaser.com)
- Laser cutting of velcro material of polyester (eurolaser.com)